Other problems for high school olympiads
Many of these problems used to be my favorites when in high school. Such problems were usually given at physics contests of different levels, or in extracurricular classes. Most of them don't even require undergraduate calculus, but some are not very easy to crack. I translated them from Russian, a large number of them being from the books by Savchenko and Bukhovtsev and other ones were created by professors of the University of Nizhny Novgorod. I use some of these when teaching college freshmen here at Auburn.The Talents of the Nizhny Novgorod Land annual olympiad (2004 - 2005)
This olympiad is conducted in the UNN (rus | eng) in winter time every year and is intended to attract gifted high school students from small towns and villages of the Nizhny Novgorod region. Their website is here (Russian; Google English translation here). You can see the new problems and browse the archive of old ones.
| 1. A wheel is rolling on a horizontal surface without sliding; the acceleration of the center of the wheel is a0. Find the acceleration of the highest point of the wheel at the moment when the magnitude of the acceleration of its lowest point becomes a0. | |
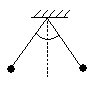 |
2. Two balls of mass m each and of the same charge are suspended on the strings of equal length L and are held at the position when the angles that the strings make with the vertical are equal and are less than 60°. After they were released, their speeds achieved the maximum at the moment when the angle between the strings was 120°. Find the charge of each ball. |
| 3. During compression of the gas in a vessel under a piston from volume 2V down to V part of the gas leaked outside and the temperature of the rest of the gas increased 1.5 times. The pressure in the vessel stayed constant and equal p at all times. What was the work of the rest of the gas during the whole process? | |
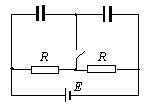 |
4. In the circuit (see figure) R = 6 Ω, E = 12 V, the capacitance of one capacitor is twice as big as of the other. Neglecting the internal resistance of the battery, find the current through the battery at the moment right after turning on the switch. |
School 40 of Nizhny Novgorod physics contests (1995 - 1998)
A stone thrown with the initial speed v0 makes a parabolic trajectory. A bird is flying along the same trajectory with the constant speed v0. What is the bird's acceleration in the highest point? (8th grade)
| A ball is elastically bouncing in the spheric hollow hitting it in two points at the same level (see the figure). The flight time from the left to the right is T1, from the right to the left T2. Find the radius of the hollow. (9th - 10th grade) | 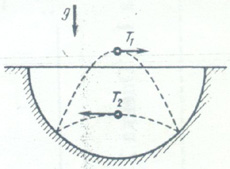 |
A stationary frictionless hemisphere of radius R is on a horizontal table. A small object is on top of the hemisphere. Due to an infinitesimally small displacement it starts sliding down, hits the table and elastically bounces. What is the maximum height above the table it will then achieve? (9th grade)
A pendulum consisting of a small object of mass m suspended on an ideal string is rotated in the vertical plane. What is the difference in the tensions of the string at the lowest and highest points? (9th grade)
A cylindric piece of ice was placed on the bottom of the vessel of the height H. It turned out that with it the vessel could accept the same amount of kerosene as with the completely melted ice. Find the height of the vessel. Water and kerosene densities are known. (9th grade)
What should the initial speed of the stone be so that having been thrown upward from the ground, it travels 2/3 of its whole way (up and down) during the last secong before hitting the ground? (9th grade)
| A uniform disk is given the angular speed around the horizontal axis (see the figure). Then a bar AB is carefully placed on it so that the former made the angle α with the level. There is friction only between the disk and the bar, the coefficient of friction is μ. Let n1 and n2 be the number of revolutions until it stops when rotating clockwise and counterclockwise accordingly with the same initial angular speed. Find q=n1/n2 (9th grade) | 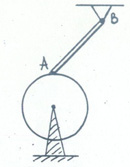 |
A body thrown upward fell down in 3 s. It traveled the first half of the way in 2 s. Find the highest point of its trajectory. Ignore air resistance. (9th grade)
A small body of the mass m is put on a horizontal wire ring of the radius R which is stuck so that it would not move. At some moment the body is given the speed v0. Find the force acting upon the body from the ring at the two moments: right after the motion begins and before the halt. The friction coefficient between the body and the ring is μ. (10th grade)
Two identical balls of masses m1 and m2 are connected with a string the length of which is much greater than the radius of the balls. Find the tension of the string during the fall in the air after a long time. (10th grade)
A boy is 200 m far from the straight highway. There is a bus going on the highway and its speed is 10 m/s. What should the minimum distance be between the boy and the bus so that he could get on it. The boy runs with the speed of 5 m/s. (9th grade)
Two balls are thrown toward each other with the same initial speed: one is thrown vertically upward from the ground, the other vertically downward from the height H. Find their initial speed if one of the balls had traveled the distance H/3 before they collided. (9th grade)
A ball was pushed horizontally with the kinetic energy 45 J. At the moment of falling into the sand its speed had the 30 degrees angle with the level. Find the heat energy emitted after the collision. The ball was not rotating in its flight. (9th grade)
